在看 code 時, 時常會遇到 afFrameCount, afLatency, afSampleRate, minBufCount, period_size, period_count ... 等等, 在本文章中會去說明各個意義和它們之間存在著什麼關係. 其實, 網路上已經有很多前輩分享相關資訊, 小弟在此做一個小整理.
[參考]
- http://m.blog.csdn.net/blog/njuitjf/9945749
- http://blog.csdn.net/azloong/article/details/17614859
- http://www.mediacollege.com/audio/01/sound-waves.html
- http://www.divediscover.whoi.edu/expedition12/hottopics/sound.html
- http://streaming.wisconsin.edu/creation/st_tech/audio_editing_SF2.html
- http://www.ni.com/white-paper/3016/zht/
- http://terms.naer.edu.tw/detail/1283354/
- https://documentation.apple.com/en/finalcutpro/usermanual/index.html#chapter=52%26section=7%26tasks=true
- http://techpubs.sgi.com/library/tpl/cgi-bin/getdoc.cgi?coll=0650&db=bks&srch=&fname=/SGI_Developer/DMSDK_PG/sgi_html/ch08.html
- http://alsa.opensrc.org/Frame
[文章目錄]
- sound wave
- wave length 和頻率 (frequency)
- sampling rate
- Nyquist sampling theorem
- bit depth
- channel
- frame
[sound wave]
聲音在透過空氣傳播的過程中, 正如上圖所示, 呈現疏密的現象, 我們可以用 sin wave 來呈現此現象, 波峰代表空氣最密集的那個點, 波谷代表空氣最稀疏的那個點.
[wave length 和 頻率]
而一個週期(例如上圖, 波峰到波峰)的長度, 我們稱為波長 ( wave length). 那頻率就是一秒內有多少個週期, 上圖的頻率就是 1k Hz, 因為一個週期要花費 1 ms , 而 1 second = 1000 ms, 所以, 一秒鐘就可以產生 1000 次週期, 換句話說, 頻率就是 1k Hz.
上圖中, 上半部所示的頻率(F1)就小於下半部所示的頻率(F2), 也就是 F1 < F2. 從這圖, 我們也可以發現, 頻率越高, 其波長就越短.
[ sampling rate ]
接下來討論 sampling rate, 為了數位儲存, 我們需要將聲音這樣的類比訊號轉成數位訊號, 所以需要透過採樣(sampling)來達成此目的, 從上圖可以看出, 採樣越多就越能貼近原本的訊號. 也因為採樣越多, 同樣一段音樂, 就需要更多的儲存空間, 換句話說, 針對同樣一段類比訊號, 採樣頻率越高, 轉出的數位檔案就會越大.
在這裡還有一個重點需要注意, 也就是在做 sampling rate 的轉換, 也會影響所需 buffer 的大小, 也就是說, 當在升頻 ( upsampling) 的動作時, 所需的 buffer 也要一起加大, 反之亦然.
[ Nyquist sampling theorem]
說到 sampling rate, 就必須提到 Nyquist sampling theorem: 對一類比信號取樣後,若要能夠完全還原原信號而不引起任何誤差, 則取樣速率必須大於等於輸入信號最大頻率的兩倍. 換句話說, 如果要正確採樣(也就是能夠還原相同頻率的訊號), 針對 1k Hz 頻率的聲音, 採樣頻率就必須要大於等於2k Hz.
B 的採樣頻率( Fs )等於該聲音的頻率(f)的兩倍, 也就是 Fs = 2f , 也就是符合 Nyquist sampling theorem 的最低需求, 所以, 當要還原波型時, 就形成一條鋸齒狀, 雖然聲音聽起來有點不一樣, 但至少, 聲音頻率是對的.
C 的採樣頻率( Fs )等於該聲音的頻率(f)的4/3倍, 也就是 Fs = 4/3f , 不符合 Nyquist sampling theorem 的最低需求, 所以, 當要還原波型時, 就形成一條大鋸齒狀, 聲音頻率是錯的.
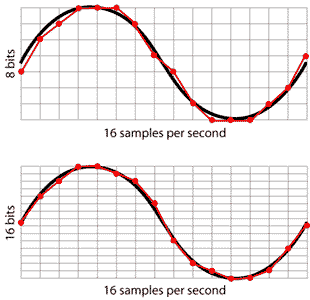
[ bit depth ]
接下來探討一下 bit depth, 如上圖, 同樣的 sampling rate, 但是, bit depth 不同, 上面是 8 bits, 下面是 16 bits, 我們可以發現, bit depth 越大, 越能貼近原本的訊號, 但是, 其檔案大小也就越大.
從上圖可知, 當 bit depth 越大, 所能表現的動態範圍也就越多.
[ channel ]
mono 為單聲道, stereo 為雙聲道或又稱立體聲. 同樣地, 針對一段聲音進行錄音( 相同的條件下), 雙聲道的資料量, 是單聲道的兩倍.
[ frame ]
構成一個聲音的最小單位, 也就是一組 samples, 而這也跟 channel 息息相關.
單聲道 ( mono ) = 1 sample = 1 frame ;
雙聲道 ( stereo) = 2 samples = 1 frame;
5.1聲道(左, 中央, 右, 右後, 左後, 低音) = 6 samples = 1 frame
所以, frame size 的計算公式如下
以下是節錄至 alsa.opensrc.org 關於 frame 的定義, 供大家參考
A frame is a set of samples, one per channel, at a particular instant in time. For stereophonic audio, a frame consists of two samples. For Dolby 5.1 Surround Sound, a frame would consist of six samples (left channel, center channel, right channel, rear right, rear left, and the low frequency channel). For monophonic audio, a frame is equivalent to one sample.







沒有留言:
張貼留言